利用寒潮后存活果穗比例评价枇杷幼果抗冻性

doi:10.16420/j.issn.0513-353x.2023-0992

摘要/Abstract

摘要：

以1个枇杷（Eriobotrya japonica）杂交后代群体为材料，利用初春果实膨大期间受冻死亡的幼果与存活幼果在果形上的明显差异，调查了遭受3次寒潮后幼果存活情况，通过计算单株的存活幼果数量（X）、果穗存活幼果平均数（Y）和自定义的存活果穗比例（Z）得到3个数据样本，用于表征群体中单株的抗冻性。样本的峰度、偏度和概率密度分布函数表明，Z较X、Y更接近正态分布，经过Box-Cox变换后Y和Z变量可通过Shapiro-Wilk测验，符合正态分布。进一步利用自定义的变量S评估不同参数取值下Y和Z变量符合正态分布的程度，确定了定义Y和Z变量所用参数的最佳取值。结果表明，参数a（预期产量）= 4、参数b（单株果穗数量）= 12时，得到的果穗存活幼果平均数（Y）和存活果穗比例（Z）数据样本在最大程度符合正态分布的同时保留了最大的样本容量，此时Y变量对应的Box-Cox变换形式没有实际意义，而Z变量的变换类型恰好为对数变换。结果表明，基于恢复生长法的枇杷幼果抗冻性新指标“存活果穗比例（Z）”可同时体现抗冻性与产量两个维度的信息，且数据获取简单高效，适合大规模枇杷杂交后代抗冻性评价。

关键词: 枇杷, 育种, 幼果, 恢复生长法, 抗冻性, 评价, 正态分布

Abstract:

This study utilized a hybrid offspring population as its experimental material. The survival of young fruits was investigated based on conspicuous differences in fruit size between frozen-injured and surviving young fruits during the fruit enlargement period. The number of survived young fruits per plant（variable X），the average number of survived young fruits per fruit cluster（variable Y），and the percentage of survived fruit clusters（variable Z）were custom-defined and transformed into three data samples. The kurtosis，skewness，and probability density distribution functions of each sample indicated that variable Z exhibited a closer approximation to a normal distribution compared with X or Y. Following Box-Cox transformation，variables Y and Z successfully passed the Shapiro-Wilk test，confirming their adherence to a normal distribution. The optimal values for parameters used in the definitions of Y and Z were determined by introducing the variable S，which assessed the degree to which the data conformed to a normal distribution and maintained a relatively large sample size. The findings revealed that setting parameter a（the expected yield）to 4 and parameter b（the number of fruit clusters）to 12 yielded data samples of the average number of survived fruit clusters（Y）and the percentage of survived fruit clusters（Z）that most closely aligned with a normal distribution while maximizing the sample size. At this juncture，the Box-Cox transformation of the（Y）variable was deemed inconsequential，whereas the transformation of the（Z）variable coincidentally corresponded to a logarithmic transformation. The results of this study suggest that the percentage of survived fruit clusters（Z）can effectively reflect both freezing tolerance and yield，with data acquisition being simple and efficient，thus rendering it suitable for large-scale freezing tolerance evaluation in loquat hybrid offspring.

Key words: loquat, breeding, young fruit, recovery growth method, freezing tolerance, evaluation, normal distribution

葛航, 李晓颖, 王志轩, 朱启轩, 陈俊伟, 徐红霞. 利用寒潮后存活果穗比例评价枇杷幼果抗冻性[J]. 园艺学报, 2024, 51(12): 2895-2912.

GE Hang, LI Xiaoying, WANG Zhixuan, ZHU Qixuan, CHEN Junwei, XU Hongxia. Evaluation of Freezing Tolerance in Loquat Young Fruit Based on the Survival Percentage of Fruit Clusters After Cold Spell[J]. Acta Horticulturae Sinica, 2024, 51(12): 2895-2912.

图/表 13

图1 寒潮后枇杷存活幼果与死亡幼果

Fig. 1 The dead and live young fruits of loquat after cold wave

表1 寒潮后枇杷单株存活幼果数量（X）、果穗存活幼果平均数（Y）和单株存活果穗比例（Z）的统计特征

Table 1 Statistical characteristics of variable X（number of survived young fruits），Y（average number of survived young fruits per fruit cluster）and Z（percentage of viable fruit clusters per plant）of loquat after cold spell

变量 Variable	样本数量 Sample size	最小值 Min.	最大值 Max.	中位数 Median	均值 Mean	方差 Variance	偏度 Skewness	峰度 Kurtosis
X	374	0	442	12	23.6	38.8	5.95	56.1
Y（b = 1）	349	0	6.33	1	1.32	1.24	1.32	4.49
Z（a = 1，b = 1）	331	0.03	1	0.5	0.49	0.27	0.24	2.05

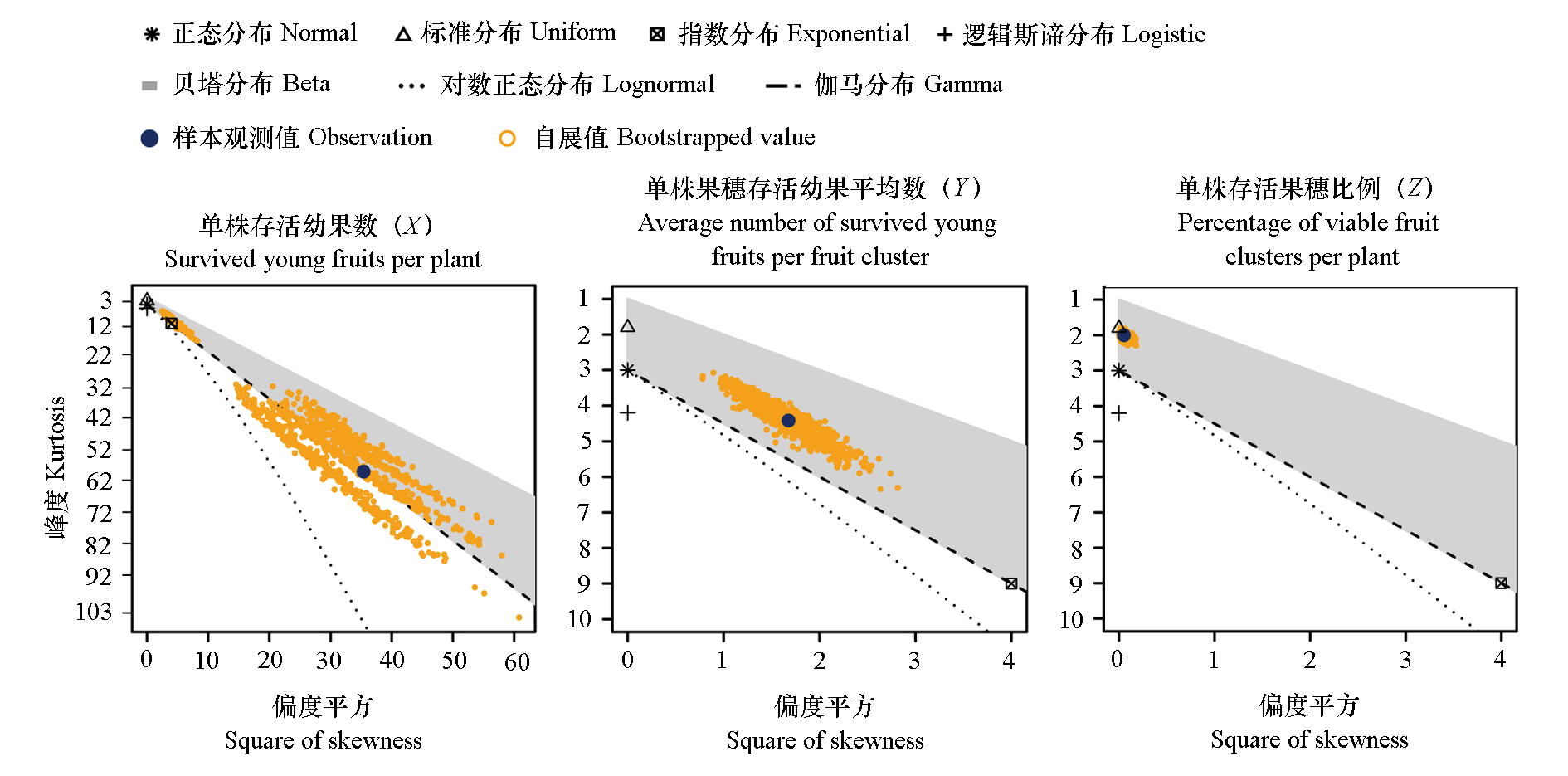
图2 寒潮后枇杷单株存活幼果数（X）、果穗存活幼果平均数（Y）、单株存活果穗比例（Z）的偏度、峰度与常见分布类型比较

Fig. 2 The skewness and kurtosis plot for variable X（survived young fruits per plant），variable Y（average number of survived young fruits per fruit cluster）and variable Z（percentage of viable fruit clusters per plant）of loquat after cold spell

表2 不同参数b下花序存活幼果平均数（Y）的统计特征分析及正态分布检验

Table 2 Statistical characteristics and Shapiro test result of variable Y（average number of surviving young fruits per inflorescence）with different value of parameter b

b	样本数量 Sample size	最大值 Max.	中位数 Median	均值 Mean	方差 Variance	偏度 Skewness	峰度 Kurtosis	Shapiro测试 W值	Shapiro测试 P值
1	374	6.33	1	1.28	1.24	1.29	4.42	0.872	4.99 × 10^-17
2	349	6.33	1	1.32	1.24	1.32	4.49	0.872	2.03 × 10^-16
3	337	6.33	1	1.32	1.21	1.33	4.53	0.874	5.38 × 10^-16
4	322	6.33	1	1.30	1.18	1.37	4.79	0.872	1.04 × 10^-15
5	308	6.33	1	1.32	1.20	1.38	4.77	0.872	2.39 × 10^-15

表3 不同参数a、b下单株存活花序比例（Z）的统计特征分析及正态分布检验

Table 3 Statistical characteristics and Shapiro test result of variable Z（percentage of viable inflorescences per plant）with different value of parameter a and b

a	b	样本数量 Sample size	最大值 Max.	中位数 Median	均值 Mean	方差 Variance	偏度 Skewness	峰度 Kurtosis	Shapiro测试 W值	Shapiro测试 P值
1	1	374	1	0.429	0.437	0.303	0.228	2.00	0.950	6.30×10^-10
1	2	349	1	0.440	0.446	0.286	0.202	2.07	0.963	9.31×10^-8
1	3	337	1	0.440	0.447	0.278	0.195	2.08	0.967	5.39×10^-7
1	4	322	1	0.441	0.444	0.271	0.175	2.06	0.969	1.88×10^-6
1	5	308	1	0.441	0.446	0.269	0.171	2.05	0.969	3.01×10^-6
2	1	374	1	0.222	0.284	0.271	0.933	3.10	0.889	8.68×10^-16
3	1	374	1	0.111	0.186	0.218	1.47	4.92	0.817	2.82×10^-16
4	1	374	0.875	0.0617	0.123	0.166	1.75	5.88	0.760	5.72×10^-23
5	1	374	0.875	0.00943	0.0840	0.136	2.25	8.75	0.678	4.54×10^-26

表4 寒潮后枇杷存活幼果数量（X）、果穗存活幼果平均数（Y）和单株存活果穗比例（Z）Shapiro-Wilk测验结果

Table 4 Shapiro-Wilk test for variable X（survived young fruits per plant），variable Y（average number of survived young fruits per fruit cluster）and variable Z（percentage of viable fruit clusters per plant）of loquat after cold spells

变量 Variable	W值 W value	P值 P value
X	0.532	2.50 × 10^-30
Y（b = 1）	0.855	1.87 × 10^-17
Z（a = 1，b = 1）	0.960	6.36 × 10^-8

图3 寒潮后枇杷单株存活幼果数（X）、果穗存活幼果平均数（Y）、单株存活果穗比例（Z）样本数据的正态分布拟合情况红色实线代表理论值，柱子和点代表实际值。参数a：预期产量；参数b：单株花序总量。下同。

Fig. 3 Goodness-of-fit plots for the normal distribution that fitted to variable X（survived young fruits per plant），variable Y （average number of survived young fruits per fruit cluster）and variable Z（percentage of viable fruit clusters per plant）of loquat after cold spell Red solid lines indicate the theoretical value and columns or dots represent the empirical value. Parameter a means the expected yield and b means the total number of flower clusters. The same below.

表5 Box-Cox变换后枇杷存活幼果数量（X）、果穗存活幼果平均数（Y）和单株存活果穗比例（Z）的Shapiro-Wilk测验结果

Table 5 Shapiro-Wilk test for variable X（number of survived young fruits），Y（average number of survived young fruits per fruit cluster）and Z（percentage of viable fruit clusters per plant）after Box-Cox transformation

变量 Variable	参数a Parameter a	参数b Parameter b	偏度 Skewness	峰度 Kurtosis	λ值 λ value	W值 W value	P值 P value
X^T			0.0036	2.79	0.09	0.985	1.50 × 10^-3
Y^T		1	-0.070	2.48	0.29	0.992	9.25 × 10^-2
Y^T		2	-0.050	2.49	0.28	0.993	0.114
Y^T		3	-0.060	2.50	0.28	0.993	0.118
Y^T		4	-0.050	2.53	0.28	0.993	0.181
Y^T		5	-0.060	2.53	0.28	0.993	0.154
Y^T		6	-0.050	2.54	0.29	0.993	0.209
Y^T		7	-0.060	2.55	0.28	0.993	0.247
Y^T		8	-0.060	2.57	0.29	0.993	0.267
Y^T		9	-0.050	2.65	0.29	0.994	0.357
Y^T		10	-0.040	2.68	0.30	0.993	0.364
Y^T		11	-0.040	2.69	0.29	0.990	0.430
Y^T		12	-0.050	2.69	0.28	0.990	0.460
Y^T		13	-0.060	2.63	0.28	0.990	0.380
Y^T		14	-0.060	2.62	0.29	0.990	0.380
Y^T		15	-0.050	2.61	0.29	0.990	0.340
Z^T	1	1	-0.15	2.11	0.62	0.972	4.19 × 10^-6
Z^T	1	2	-0.15	2.14	0.62	0.975	2.18 × 10^-5
Z^T	1	3	-0.15	2.12	0.63	0.976	3.82 × 10^-5
Z^T	1	4	-0.16	2.11	0.63	0.975	4.07 × 10^-5
Z^T	1	5	-0.16	2.09	0.64	0.974	3.77 × 10^-5
Z^T	1	6	-0.17	2.10	0.66	0.974	5.31 × 10^-5
Z^T	1	7	-0.17	2.12	0.64	0.975	1.06 × 10^-4
Z^T	1	8	-0.17	2.10	0.65	0.974	9.52 × 10^-5
Z^T	1	9	-0.16	2.14	0.66	0.976	2.40 × 10^-4
Z^T	1	10	-0.16	2.15	0.65	0.976	4.28 × 10^-4
Z^T	1	11	-0.16	2.17	0.63	0.977	9.27 × 10^-4
Z^T	1	12	-0.16	2.13	0.61	0.975	7.03 × 10^-4
Z^T	1	13	-0.16	2.10	0.60	0.973	6.24 × 10^-4
Z^T	1	14	-0.16	2.10	0.61	0.973	7.18 × 10^-4
Z^T	1	15	-0.17	2.10	0.59	0.972	1.13 × 10^-3
Z^T	1	1	-0.15	2.11	0.62	0.972	4.19 × 10^-6
Z^T	2	1	-0.08	2.30	0.33	0.984	2.08 × 10^-3
Z^T	3	1	-0.04	2.30	0.17	0.988	2.54 × 10^-2
Z^T	4	1	-0.01	2.36	0.09	0.987	3.32 × 10^-2
Z^T	5	1	0.02	2.12	-0.05	0.980	8.94 × 10^-3
Z^T	6	1	0.01	2.19	-0.05	0.981	4.27 × 10^-2
Z^T	7	1	0.00	2.34	0.00	0.985	0.245
Z^T	8	1	0.00	2.51	-0.08	0.987	0.546
Z^T	9	1	0.02	2.67	-0.18	0.988	0.816
Z^T	10	1	0.01	2.50	-0.12	0.987	0.868
Z^T	11	1	0.03	2.48	-0.20	0.982	0.828
Z^T	12	1	0.15	1.88	-0.46	0.957	0.386
Z^T	13	1	0.14	1.57	-0.35	0.924	0.152
Z^T	14	1	-0.16	1.33	0.35	0.905	0.212
Z^T	15	1	-0.45	3.44	1.27	0.979	0.960

表5 Box-Cox变换后枇杷存活幼果数量（X）、果穗存活幼果平均数（Y）和单株存活果穗比例（Z）的Shapiro-Wilk测验结果

变量 Variable	参数a Parameter a	参数b Parameter b	偏度 Skewness	峰度 Kurtosis	λ值 λ value	W值 W value	P值 P value
X^T			0.0036	2.79	0.09	0.985	1.50 × 10^-3
Y^T		1	-0.070	2.48	0.29	0.992	9.25 × 10^-2
Y^T		2	-0.050	2.49	0.28	0.993	0.114
Y^T		3	-0.060	2.50	0.28	0.993	0.118
Y^T		4	-0.050	2.53	0.28	0.993	0.181
Y^T		5	-0.060	2.53	0.28	0.993	0.154
Y^T		6	-0.050	2.54	0.29	0.993	0.209
Y^T		7	-0.060	2.55	0.28	0.993	0.247
Y^T		8	-0.060	2.57	0.29	0.993	0.267
Y^T		9	-0.050	2.65	0.29	0.994	0.357
Y^T		10	-0.040	2.68	0.30	0.993	0.364
Y^T		11	-0.040	2.69	0.29	0.990	0.430
Y^T		12	-0.050	2.69	0.28	0.990	0.460
Y^T		13	-0.060	2.63	0.28	0.990	0.380
Y^T		14	-0.060	2.62	0.29	0.990	0.380
Y^T		15	-0.050	2.61	0.29	0.990	0.340
Z^T	1	1	-0.15	2.11	0.62	0.972	4.19 × 10^-6
Z^T	1	2	-0.15	2.14	0.62	0.975	2.18 × 10^-5
Z^T	1	3	-0.15	2.12	0.63	0.976	3.82 × 10^-5
Z^T	1	4	-0.16	2.11	0.63	0.975	4.07 × 10^-5
Z^T	1	5	-0.16	2.09	0.64	0.974	3.77 × 10^-5
Z^T	1	6	-0.17	2.10	0.66	0.974	5.31 × 10^-5
Z^T	1	7	-0.17	2.12	0.64	0.975	1.06 × 10^-4
Z^T	1	8	-0.17	2.10	0.65	0.974	9.52 × 10^-5
Z^T	1	9	-0.16	2.14	0.66	0.976	2.40 × 10^-4
Z^T	1	10	-0.16	2.15	0.65	0.976	4.28 × 10^-4
Z^T	1	11	-0.16	2.17	0.63	0.977	9.27 × 10^-4
Z^T	1	12	-0.16	2.13	0.61	0.975	7.03 × 10^-4
Z^T	1	13	-0.16	2.10	0.60	0.973	6.24 × 10^-4
Z^T	1	14	-0.16	2.10	0.61	0.973	7.18 × 10^-4
Z^T	1	15	-0.17	2.10	0.59	0.972	1.13 × 10^-3
Z^T	1	1	-0.15	2.11	0.62	0.972	4.19 × 10^-6
Z^T	2	1	-0.08	2.30	0.33	0.984	2.08 × 10^-3
Z^T	3	1	-0.04	2.30	0.17	0.988	2.54 × 10^-2
Z^T	4	1	-0.01	2.36	0.09	0.987	3.32 × 10^-2
Z^T	5	1	0.02	2.12	-0.05	0.980	8.94 × 10^-3
Z^T	6	1	0.01	2.19	-0.05	0.981	4.27 × 10^-2
Z^T	7	1	0.00	2.34	0.00	0.985	0.245
Z^T	8	1	0.00	2.51	-0.08	0.987	0.546
Z^T	9	1	0.02	2.67	-0.18	0.988	0.816
Z^T	10	1	0.01	2.50	-0.12	0.987	0.868
Z^T	11	1	0.03	2.48	-0.20	0.982	0.828
Z^T	12	1	0.15	1.88	-0.46	0.957	0.386
Z^T	13	1	0.14	1.57	-0.35	0.924	0.152
Z^T	14	1	-0.16	1.33	0.35	0.905	0.212
Z^T	15	1	-0.45	3.44	1.27	0.979	0.960

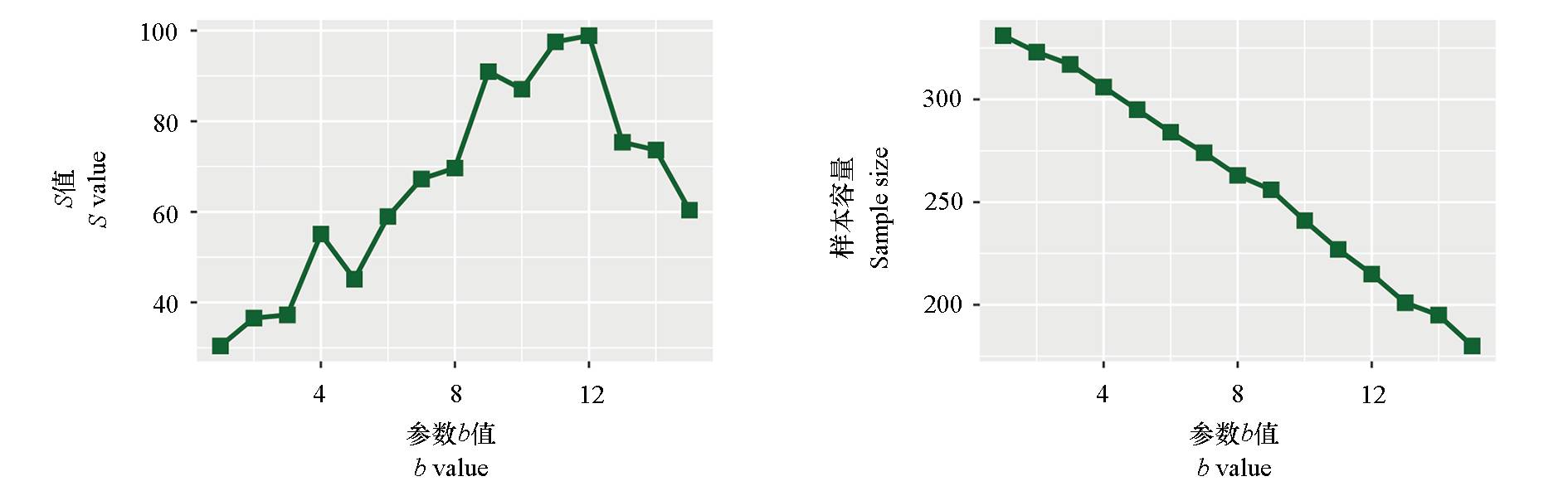
图4 参数b（单株果穗数量）对果穗存活幼果平均数变量（Y）的S值和样本容量的影响

Fig. 4 Effect of parameter b（the total number of flower clusters on a single plant）on the variable S value and sample size of average number of survived young fruits per fruit cluster（variable Y）

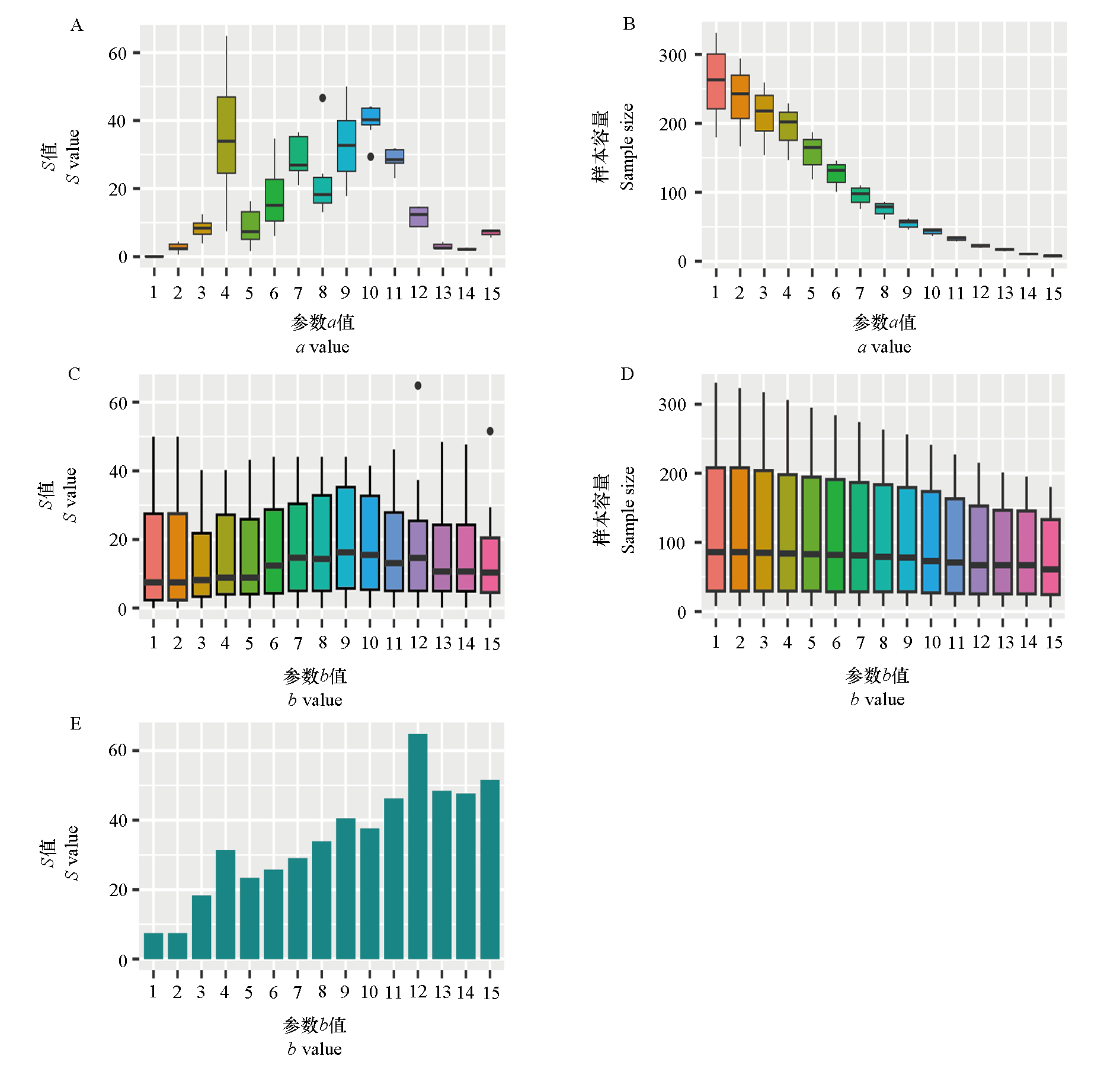
图5 参数a、b对单株存活果穗比例（Z）变量S值和样本容量的影响 A：参数a不同取值下Z变量S值的变化；B：参数a不同取值下Z变量样本容量的变化；C：参数b不同取值下Z变量S值的变化；D：参数b不同取值下Z变量样本容量的变化；E：参数a取值为4时参数b不同取值对应的Z变量S值。

Fig. 5 Influence of parameters a and b on the variable S and sample size of the variable Z（percentage of viable fruit clusters per plant） A：Variation in S value of variable Z under different values of parameter a；B：Variation in sample size of variable Z under different values of parameter a；C：Variation in S value of variable Z under different values of parameter b；D：Variation in sample size of variable Z under different values of parameter b；E：Effect of different values of parameter b on S value of variable Z when parameter a is fixed at the value of 4.

表6 单株存活幼果数量（X）、果穗存活幼果平均数（Y）和单株存活果穗比例（Z）Box-Cox变换中的λ值确定

Table 6 The λ calculation of variants X，Y and Z which is used for Box-Cox transformation

变量 Variable	最佳λ值 Optimal λ value	采用λ值 selected λ value	变换类型 Type of trans- formation	变换后偏度 Skewness after transformation	变换后峰度 Kurtosis after transformation	变换后W值 W value after transformation	变换后P值 P value after transformation
X^T	0.09	0.09	无None	-0.860	3.70	0.951	1.21 × 10^-6
Y^T（b = 12）	0.28	0.28	无None	-0.046	2.69	0.993	0.463
Z^T（a = 4，b = 12）	-0.01	0	对数变换 Logarithm transformation	0.012	2.60	0.991	0.383

图6 Box-Cox变换后果穗存活幼果平均数（Y）样本数据的正态分布拟合情况

Fig. 6 Goodness-of-fit plots for the normal distribution that fitted to variable Y after Box-Cox transformation

图7 Box-Cox变换后单株存活果穗比例（Z）样本数据的正态分布拟合情况

Fig. 7 Goodness-of-fit plots for the normal distribution that fitted to variable Z after Box-Cox transformation

参考文献 45

[1]	Boinot M, Karakas E, Koehl K, Pagter M, Zuther E. 2022. Cold stress and freezing tolerance negatively affect the fitness of Arabidopsis thaliana accessions under field and controlled conditions. Planta, 255 (2):39.
[2]	Burr K E, Hawkins C D B, L Hirondelle S J, Binder W D, George M F, Repo T. 2001. Methods for measuring cold hardiness of conifers. Dordrecht:Springer Netherlands:369-401.
[3]	Chen Fangyong, Wang Yin, Ni Haizhi, Yan Bangguo. 2019. The comparison of physiological indicators under cold stress in different locations for “Ruantiaobaisha”loquat. South China Fruits, 48 (1):36-40. (in Chinese)
	陈方永, 王引, 倪海枝, 颜帮国. 2019. “软条白沙”枇杷不同立地条件下冻害胁迫生理指标比较. 中国南方果树, 48 (1):36-40.
[4]	Chen Junwei, Sun Jun, Li Xiaoying, Xu Hongxia, Zhou Xiaoyin, Jiang Luhua. 2017. Discussion on late flowering cultivation techniques to avoid frost in white-fleshed loquat. Journal of Zhejiang Agricultural Sciences, 58 (3):417-419,425. (in Chinese)
	陈俊伟, 孙钧, 李晓颖, 徐红霞, 周晓音, 姜路花. 2017. 白肉枇杷晚花避冻栽培技术探讨. 浙江农业科学, 58 (3):417-419,425. doi: 10.16178/j.issn.0528-9017.20170316
[5]	Cui Long, Wang Xuesong, Tan Rui, Zhang Yanbo, Chen Lei. 2023. Optimization and evaluation of methods for identifying cold hardiness of apricot germplasm branches under natural wintering conditions in cold regions. Agriculture and Technology, 43 (21):72-75. (in Chinese)
	崔龙, 王雪松, 谭瑞, 张艳波, 陈蕾. 2023. 寒地杏种质自然越冬条件下枝条抗寒性鉴定方法优化及评价. 农业与技术, 43 (21):72-75.
[6]	Chen M, Guo H, Chen S, Li T, Li M, Rashid A, Xu C, Wang K. 2019. Methyl jasmonate promotes phospholipid remodeling and jasmonic acid signaling to alleviate chilling injury in peach fruit. Journal of Agricultural and Food Chemistry, 67 (35):9958-9966. doi: 10.1021/acs.jafc.9b03853 pmid: 31419123
[7]	Delignette-Muller M L, Dutang C. 2015. Fitdistrplus:an R package for fitting distributions. Journal of Statistical Software, 64 (4):1-34.
[8]	Huang H, Guo L, Wang L, Wang H, Ma S, Jiang Y, Qu H. 2019. 1-Methylcyclopropene(1-MCP)slows ripening of kiwifruit and affects energy status,membrane fatty acid contents and cell membrane integrity. Postharvest Biology and Technology,156:110941.
[9]	Fan Kaifeng, Li Qingbin, Fang Yue, Huang Xin, Qin Benben, Chen Lei, Jin Zhifeng. 2022. Impact of meteorological disasters on loquat in Ningbo and suggested defensive measures. Journal of Zhejiang Agricultural Sciences, 63 (8):1818-1820. (in Chinese)
	范凯锋, 李清斌, 房玥, 黄新, 秦奔奔, 陈磊, 金志凤. 2022. 气象灾害对宁波枇杷的影响及防御措施建议. 浙江农业科学, 63 (8):1818-1820.
[10]	Jian Dan, Lu Tao, Shao Xiaowei, Jin Yang. 2022. Preliminary study on a forecasting model for low-temperature frost damage during the flowering and fruiting periods of loquat in Lanxi. Journal of Zhejiang Agricultural Sciences, 63 (7):1482-1486,1494. (in Chinese)
	简单, 陆韬, 邵小卫, 金杨. 2022. 兰溪枇杷花果期低温冻害预报模型初探. 浙江农业科学, 63 (7):1482-1486,1494. doi: 10.16178/j.issn.0528-9017.20213010
[11]	Jin Ruiping, Wang Huakun, Wang Tong, Huang Zhangbing, Zhang Huanchao. 2019. Effect of exogenous SOD on cold hardiness of young loquat fruit under low-temperature stress. Jiangsu Agricultural Sciences, 47 (2):138-141. (in Chinese)
	靳瑞萍, 王化坤, 王彤, 黄长兵, 张焕朝. 2019. 低温胁迫下外源SOD对枇杷幼果抗寒性的影响. 江苏农业科学, 47 (2):138-141.
[12]	Jin Yitang, Tie Wanzhu, Feng Jiaping, Wang Fengping, Liao Lili, Wang Youfu. 2023. Preventive measures and countermeasures of low temperature freezing damage of loquat in panxi region. China Tropical Agriculture,(2):78-80. (in Chinese)
	晋一棠, 铁万祝, 冯家平, 王凤屏, 廖莉莉, 王友富. 2023. 攀西地区枇杷低温冻害预防措施与对策. 中国热带农业,(2):78-80.
[13]	Jing Peng, Lü Muwen, Sun Cuicui, Zheng Yonghua, Sun Ming. 2012. Effects of Methyl jasmonate in combination with low temperature conditioning on chilling injury and active oxygen metabolism in loquat fruits. Acta Horticulturae Sinica, 39 (3):461-468. (in Chinese)
	金鹏, 吕慕雯, 孙萃萃, 郑永华, 孙明. 2012. MeJA与低温预贮对枇杷冷害和活性氧代谢的影响. 园艺学报, 39 (3):461-468.
[14]	Kou Bin, Wang Yan, Ren Xiaoyan. 2016. Screening methods for testing cold hardiness in jujube trees. Xinjiang Farm Research of Science and Technology, 39 (2):43-45. (in Chinese)
	寇彬, 王岩, 任晓燕. 2016. 枣树抗寒性检测方法的筛选. 新疆农垦科技, 39 (2):43-45.
[15]	Li Jing. 2020. Causes and prevention strategies for loquat frost damage in Sichuan Province. Modern Agricultural Science and Technology,(1):84,86. (in Chinese)
	李靖. 2020. 四川省枇杷冻害发生原因及预防对策. 现代农业科技,(1):84,86.
[16]	Li Ling, Gui Mingchun, Guan Yan, Mao Changli, Tian Hai, Zhang Fengliang, Wu Yu, Duan An’an, Liang Guoping. 2021. Cold resistance of rubber trees(Hevea brasiliensis)by combined recovery and conductivity analysis. Chinese Journal of Tropical Crops, 42 (2):370-377. (in Chinese) doi: 10.3969/j.issn.1000-2561.2021.02.011
	李玲, 桂明春, 管艳, 毛常丽, 田海, 张凤良, 吴裕, 段安安, 梁国平. 2021. 恢复生长与电导法结合分析橡胶树抗寒性研究. 热带作物学报, 42 (2):370-377. doi: 10.3969/j.issn.1000-2561.2021.02.011
[17]	Liu Guoqiang, Wu Jincheng, Zhu Ying, Liu Meiqiong, Cai Xiaoling, Chen Liping. 2009. Effect of salicylic acid on some physiological and biochemical indexes in young loquat fruits under low temperature stress. Chinese Journal of Tropical Crops, 30 (3):254-258. (in Chinese)
	刘国强, 吴锦程, 朱颖, 刘美琼, 蔡小玲, 陈丽平. 2009. 水杨酸对低温胁迫下枇杷幼果若干生理生化指标的影响. 热带作物学报, 30 (3):254-258.
[18]	Liu H, Pei H, Jiao J, Jin M, Li H, Zhu Q, Ma Y, Rao J. 2021. 1-Methylcyclopropene treatment followed with ethylene treatment alleviates postharvest chilling injury of‘Xuxiang’kiwifruit during low-temperature storage. Food Control,130:108340.
[19]	Liu Shaojun, Niu Ying, Chen Guoping, Liu Binghao, Liu Ping, Fan Qijun. 2014. Study on determining the cold hardiness of young citrus varieties using the electrical conductivity method combined with the Logistic equation. South China Fruits, 43 (2):57-59. (in Chinese)
	刘绍俊, 牛英, 陈国平, 刘冰浩, 刘萍, 范七君. 2014. 电导法配合Logistic方程测定柑桔品种幼树抗寒性的研究. 中国南方果树, 43 (2):57-59.
[20]	Liu Zhenghai, Dong Zhigang, Li Xiaomei, Tan Min, Yang Rongzhao, Yang Zhaoliang, Tang Xiaoping. 2021. Analysis of cold resistance of wine grape based on recovery growth method. Journal of Fruit Resources, 2 (2):5-8. (in Chinese)
	刘政海, 董志刚, 李晓梅, 谭敏, 杨镕兆, 杨兆亮, 唐晓萍. 2021. 基于恢复生长法分析酿酒葡萄品种的抗寒性. 果树资源学报, 2 (2):5-8.
[21]	Lou Xiaoming. 2018. Identification of cold tolerance germplasm and the cold tolerance mechanism in loquat[Ph. D. Dissertation]. Nanjing: Nanjing Agricultural University. (in Chinese)
	娄晓鸣. 2018. 枇杷(Eriobotrya japonica Lindl.)抗寒种质鉴定及其抗寒机制[博士论文]. 南京: 南京农业大学.
[22]	Ma Y, Hu S, Chen G, Zheng Y, Jin P. 2022. Cold shock treatment alleviates chilling injury in peach fruit by regulating antioxidant capacity and membrane lipid metabolism. Food Quality and Safety, 6 (1):13-23.
[23]	Moellering E R, Muthan B, Benning C. 2010. Freezing tolerance in plants requires lipid remodeling at the outer chloroplast membrane. Science, 330 (6001):226-228. doi: 10.1126/science.1191803 pmid: 20798281
[24]	Niu Lixin, Zhang Yanlong. 1996. Discussion on methods for determining and evaluating the cold hardiness of apple varieties. Deciduous Fruits,(S1):1-2. (in Chinese)
	牛立新, 张延龙. 1996. 苹果品种抗寒性测定及其评价方法探讨. 落叶果树,(S1):1-2.
[25]	Pan Cuiping, Xie Hongjiang, Wang Yongqing, Zhang Hui, Deng Qunxian, Yang Zhiwu, Wen Lu, He Shanshan. 2019. Physiological responses and evaluation of cold resistance under cold stress for six varieties of Eriobotrya japonica(Thunb.). Chinese Journal of Tropical Crops, 40 (12):2369-2374. (in Chinese) doi: 10.3969/j.issn.1000-2561.2019.12.009
	潘翠萍, 谢红江, 王永清, 张卉, 邓群仙, 杨志武, 文露, 何珊珊. 2019. 6个枇杷品种对低温胁迫的生理响应及抗寒性评价. 热带作物学报, 40 (12):2369-2374. doi: 10.3969/j.issn.1000-2561.2019.12.009
[26]	Rasouli M, Saba M K, Ramezanian A. 2019. Inhibitory effect of salicylic acid and Aloe vera gel edible coating on microbial load and chilling injury of orange fruit. Scientia Horticulturae,247:27-34.
[27]	Tang Haixia, Yang Xuemei, Feng Lijuan, Zhu Feng, Zhou Jilei, Yin Yanlei. 2023. Analysis of freezing tolerances and physiological differences of three pomegranate cultivars during the overwintering. Acta Horticulturae Sinica, 50 (7):1563-1573. (in Chinese) doi: 10.16420/j.issn.0513-353x.2022-0551 URL
	唐海霞, 杨雪梅, 冯立娟, 朱峰, 周继磊, 尹燕雷. 2023. 3个石榴品种越冬抗寒性及生理差异分析. 园艺学报, 50 (7):1563-1573.
[28]	Wang Guoli, Guo Zhenfei. 2005. Effects of chilling stress on photosynthetic rate and the parameters of chlorophyll fluorescence in two rice varieties differing in sensitivity. Chinese Journal of Rice Science, 19 (4):381-383. (in Chinese)
	王国莉, 郭振飞. 2005. 低温对水稻不同耐冷品种幼苗光合速率和叶绿素荧光参数的影响. 中国水稻科学, 19 (4):381-383.
[29]	Wang Shanbo. 2012. Research on the extreme climate of inner Mongolia in recent fifty years by using the robust medium value method[Ph. D. Dissertation]. Yangzhou: Yangzhou University. (in Chinese)
	王善波. 2012. 利用稳健中值方法研究近50年内蒙古极端气候[博士论文]. 扬州: 扬州大学.
[30]	Wang Xiaohui, Guo Qigao, He Qiao, Yao Dan, Li Xiaolin, Xiang Suqiong, Wang Weixing, Sun Haiyan, Liang Guolu. 2012. Measurement of cold tolerance based on REC and the logistic equation in triploid loquat. Journal of Southwest China Normal University(Natural Science Edition), 37 (6):121-124. (in Chinese)
	王晓辉, 郭启高, 何桥, 姚丹, 李晓林, 向素琼, 汪卫星, 孙海艳, 梁国鲁. 2012. 电导法结合Logistic方程鉴定三倍体枇杷的抗寒性研究. 西南师范大学学报(自然科学版), 37 (6):121-124.
[31]	Wei Huabing, Chen Zhenghong, Li Guihong, Wang Xudong, Luo Xiang, Yuan Guanqiang. 2022. Occurrence and risk analysis of freezing and heat injury of loquat in Southeastern Hubei. Chinese Journal of Tropical Agriculture, 42 (3):93-99. (in Chinese)
	魏华兵, 陈正洪, 李桂红, 汪旭东, 罗翔, 袁观强. 2022. 鄂东南枇杷的冻、热害发生规律及风险分析. 热带农业科学, 42 (3):93-99.
[32]	Wisniewski M, Nassuth A, Teulières C, Marque C, Rowland J, Cao P B, Brown A. 2014. Genomics of cold hardiness in woody plants. Critical Reviews in Plant Sciences, 33 (2-3):92-124.
[33]	Wu Yao, Du Liangmin, Liu Changzheng, Zhang Jun. 2022. Application of Box-Cox transformation in the determination of extreme precipitation climate events in the Yangtze sub-basins. Torrential Rain and Disasters, 41 (1):94-100. (in Chinese)
	吴瑶, 杜良敏, 刘长征, 张俊. 2022. Box-Cox正态转换在长江子流域极端降水气候事件判定中的应用. 暴雨灾害, 41 (1):94-100.
[34]	Xiao Xiangzhen. 2011. Study on the Box-Cox transformation of the breast diameter growth model for winged elm. Forestry Science & Technology, 36 (4):35-37. (in Chinese)
	肖象珍. 2011. 翅荚木胸径生长模型的Box-Cox变换研究. 林业科技, 36 (4):35-37.
[35]	Xiao Zhijian. 2011. Improvement of the one-variable linear model for height-diameter relationship in Fujian cypress. Ningxia Journal of Agriculture and Forestry Science and Technology, 52 (7):56-57. (in Chinese)
	肖志坚. 2011. 福建柏树高—胸径一元线性模型的改进. 宁夏农林科技, 52 (7):56-57.
[36]	Xu F, Liu S, Liu Y, Xu Q, Wang S. 2019. The combined effect of ultraviolet-C irradiation and lysozyme coatings treatment on control of brown heart in Huangguan pears. Scientia Horticulturae,256:108634.
[37]	Xu Hongxia, Li Xiaoying, Chen Junwei. 2020. Studies on the amino acid metabolism and carbohydrate metabolism variation during flower development in Eriobotrya japonica. Acta Horticulturae Sinica, 47 (2):233-241. (in Chinese) doi: 10.16420/j.issn.0513-353x.2019-0271 URL
	徐红霞, 李晓颖, 陈俊伟. 2020. 枇杷花发育进程中氨基酸和碳水化合物代谢的变化. 园艺学报, 47 (2):233-241. doi: 10.16420/j.issn.0513-353x.2019-0271 URL
[38]	Xu Hongxia, Zhou Huifen, Li Xiaoying, Jiang Luhua, Chen Junwei. 2021. Comparative transcriptome analysis of different developmental stages of flowers and fruits in loquat under low temperature stress. Acta Horticulturae Sinica, 48 (9):1680-1694. (in Chinese) doi: 10.16420/j.issn.0513-353x.2021- 0219 URL
	徐红霞, 周慧芬, 李晓颖, 姜路花, 陈俊伟. 2021. 低温胁迫下枇杷不同发育阶段的花果转录组比较分析. 园艺学报, 48 (9):1680-1694. doi: 10.16420/j.issn.0513-353x.2021- 0219 URL
[39]	Yang Yonge, Zhang Xiaoyu, Liang Xiaojuan, Ma Mengyao, Wei Jianguo. 2023. Studies on the sensitivity of apple flowers and fruits to low temperatures from flowering to young fruiting stage. Acta Botanica Boreali-Occidentalia Sinica, 43 (10):1694-1703. (in Chinese)
	杨永娥, 张晓煜, 梁小娟, 马梦瑶, 卫建国. 2023. 苹果花期至幼果期花朵和果实对低温的敏感性研究. 西北植物学报, 43 (10):1694-1703.
[40]	Zhang Dongya, Zhao Lei, Sun Shouwen, Tao Xiudong. 2010. Preliminary assessment of cold hardiness in six hybrid varieties of dense-leaf poplar × Tamarisk. Xinjiang Agricultural Sciences, 47 (4):711-714. (in Chinese)
	张东亚, 赵蕾, 孙守文, 陶秀冬. 2010. 密叶杨 × 胡杨6个杂交种抗寒性的初步鉴定. 新疆农业科学, 47 (4):711-714.
[41]	Zhang Heying. 2007. The effect of cold stress on ultrastructure and physiological metabolism in Eriobotrya japonica Lindl.[Ph. D. Dissertation]. Fuzhou: Fujian Agriculture and Forestry University. (in Chinese)
	张贺英. 2007. 低温胁迫对枇杷超微结构及生理代谢的影响[博士论文]. 福州: 福建农林大学.
[42]	Zhang Lixin, Wang Qingjie, Chen Jilong. 2019. Analysis the relationship between Populus Euphratica’s volume and DBH in alar based on Box-Cox transform. Mathematics in Practice and Theory, 49 (3):215-222. (in Chinese)
	张立欣, 王庆杰, 陈纪龙. 2019. 基于Box-Cox变换的阿拉尔地区胡杨材积与胸径的关系分析. 数学的实践与认识, 49 (3):215-222.
[43]	Zhang Jiaying, Zhang Xueying, An Haishan, Jiang Shuang, Xu Fangjie. 2021. Physiological evaluation on cold resistance of five loquat varieties(lines)(Eriobotrya japonica Thunb.). Acta Agriculturae Shanghai, 37 (5):39-46. (in Chinese)
	章加应, 张学英, 安海山, 蒋爽, 徐芳杰. 2021. 5份枇杷品种(系)的抗寒性生理评价. 上海农业学报, 37 (5):39-46.
[44]	Zhao Deying, Cheng Cungang, Zhang Shaoyu, Zhang Yanchang, Yuan Jicun, Hou Guixue. 2010. Advance on the response of fruit tree on the chilling and cold resistance appraisal system. Forest by-Product and Speciality in China,(6):81-84. (in Chinese)
	赵德英, 程存刚, 张少瑜, 张彦昌, 袁继存, 侯贵学. 2010. 果树对低温的响应及抗寒评价体系研究进展. 中国林副特产,(6):81-84.
[45]	Zhao Tongsheng, Zhao Guodong, Zhang Xinsheng, Li Chunmin, Fu You. 2018. Comparison of cold hardiness among several apple dwarfing rootstocks using regrowth recovery and tissue browning methods. China Fruits,(3):23-25. (in Chinese)
	赵同生, 赵国栋, 张新生, 李春敏, 付友. 2018. 应用恢复生长法和组织褐变法比较几种苹果矮化砧木抗寒性. 中国果树,(3):23-25.